二叉树

什么是二叉树

简单地理解，满足以下两个条件的树就是二叉树：

本身是有序树；

树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2；

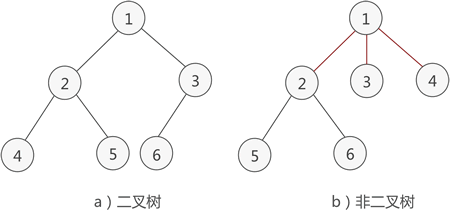
二叉树示意图

二叉树性质

  • 二叉树中，第 i 层最多有 2i-1 个结点。
  • 如果二叉树的深度为 K，那么此二叉树最多有 2K-1 个结点。
  • 二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。

性质 3 的计算方法为：对于一个二叉树来说，除了度为 0 的叶子结点和度为 2 的结点，剩下的就是度为 1 的结点（设为 n1），那么总结点 n=n0+n1+n2。
同时，对于每一个结点来说都是由其父结点分支表示的，假设树中分枝数为 B，那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的，即 B=n1+2n2。所以，n 用另外一种方式表示为 n=n1+2n2+1。
两种方式得到的 n 值组成一个方程组，就可以得出 n0=n2+1。

满二叉树

如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

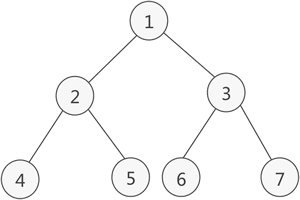
满二叉树示意图

满二叉树除了满足普通二叉树的性质，还具有以下性质：

  • 满二叉树中第 i 层的节点数为 2n-1 个。
  • 深度为 k 的满二叉树必有 2k-1 个节点 ，叶子数为 2k-1。
  • 满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。
  • 具有 n 个节点的满二叉树的深度为 log2(n+1)。

完全二叉树

如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

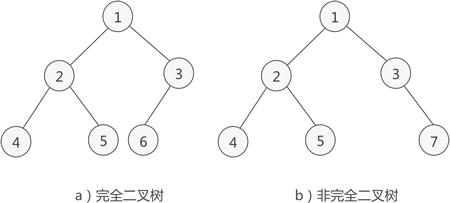
完全二叉树示意图

如图 3a) 所示是一棵完全二叉树，图 3b) 由于最后一层的节点没有按照从左向右分布，因此只能算作是普通的二叉树。

完全二叉树除了具有普通二叉树的性质，它自身也具有一些独特的性质，比如说，n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。

⌊log2n⌋ 表示取小于 log2n 的最大整数。例如，⌊log24⌋ = 2，而 ⌊log25⌋ 结果也是 2。

对于任意一个完全二叉树来说，如果将含有的结点按照层次从左到右依次标号（如图 3a)），对于任意一个结点 i ，完全二叉树还有以下几个结论成立：

  • 当 i>1 时，父亲结点为结点 [i/2] 。（i=1 时，表示的是根结点，无父亲结点）
  • 如果 2i>n（总结点的个数） ，则结点 i 肯定没有左孩子（为叶子结点）；否则其左孩子是结点 2i 。
  • 如果 2i+1>n ，则结点 i 肯定没有右孩子；否则右孩子是结点 2i+1 。

二叉树储存结构

采用链式存储二叉树时，其节点结构由 3 部分构成：

  • 指向左孩子节点的指针（Lchild）；
  • 节点存储的数据（data）；
  • 指向右孩子节点的指针（Rchild）；

表示该节点结构的 C#代码为：

1
2
3
4
5
6
7
8
9
10
11
Definition for a binary tree node.
public class TreeNode {
  	public int val;
  	public TreeNode left;
  	public TreeNode right;
  	public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
  	this.val = val;
  	this.left = left;
  	this.right = right;
  }
}

二叉树遍历

img

先序遍历：

  • 访问根节点；
  • 访问当前节点的左子树；
  • 若当前节点无左子树，则访问当前节点的右子树；

中序遍历：

  1. 访问当前节点的左子树；
  2. 访问根节点；
  3. 访问当前节点的右子树；

后续遍历：

从根节点出发，依次遍历各节点的左右子树，直到当前节点左右子树遍历完成后，才访问该节点元素。

根-> 左-> 右
左-> 根-> 右
左-> 右-> 根
根再前就是前序，在中就是中序，在最后就是后续，遍历的时候可以三个为一组比较容易看

递归写法遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//前序遍历二叉树,并将遍历的结果保存到list中
private void dfs(TreeNode node, IList<TreeNode> list)
{
    if (node == null)
    {
        return;
    }
  	list.Add(node);
    dfs(node.left, list);
    dfs(node.right, list);
}
//中序遍历二叉树,并将遍历的结果保存到list中
private void dfs(TreeNode node, IList<TreeNode> list)
{
    if (node == null)
    {
        return;
    }
    dfs(node.left, list);
    list.Add(node);
    dfs(node.right, list);
}
//后续序遍历二叉树,并将遍历的结果保存到list中
private void dfs(TreeNode node, IList<TreeNode> list)
{
    if (node == null)
    {
        return;
    }
    dfs(node.left, list);
    dfs(node.right, list);
  	list.Add(node);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
//非递归先序,要先访问根节点，然后再去访问左子树以及右子树，这明显是递归定义，但这里是用栈来实现的
//先需要先从栈顶取出节点，然后访问该节点，如果该节点不为空，则存储该节点，同时把该节点的右子树先入栈，然后左子树入栈。循环结束的条件是栈中不在有节点。
public void preOrder(TreeNode root)
{
    TreeNode cur = root;
    Stack<TreeNode> stack = new Stack<TreeNode>();
    IList<TreeNode> result = new List<TreeNode>();
  
    while (stack.Count > 0 || cur != null)
    {
        if (cur != null)
        {
            result.Add(cur);
            stack.Push(cur);
            cur = cur.left;
        }
        else
        {
            cur = stack.Pop();
            cur = cur.right;
        }
    }
}
//非递归中序
public void inOrder(TreeNode root)
{
    TreeNode cur = root;
    Stack<TreeNode> stack = new Stack<TreeNode>();
    IList<TreeNode> result = new List<TreeNode>();
  
    while (stack.Count > 0 || cur != null)
    {
        if (cur != null)
        {
            
            stack.Push(cur);
            cur = cur.left;
        }
        else
        {
            cur = stack.Pop();
          	result.Add(cur);
            cur = cur.right;
        }
    }
}
//非递归后续
public void postOrder(TreeNode root)
{
    TreeNode cur = root;
  	TreeNode p = null;
    Stack<TreeNode> stack = new Stack<TreeNode>();
    IList<TreeNode> result = new List<TreeNode>();
  
    while (stack.Count > 0 || cur != null)
    {
      	while(cur != null)
        {
          stack.Push(cur);
            cur = cur.left;
        }
      	cur = stack.Peek();
        if (cur.right != null && cur.right != p)
        {
            cur = cur.right;
        }
        else
        {
            cur = stack.Pop();
          	result.Add(cur);
            p = cur;
          	cur = null;
        }
    }
}

层次遍历：

按照二叉树中的层次从左到右依次遍历每层中的结点。具体的实现思路是：通过使用队列的数据结构，从树的根结点开始，依次将其左孩子和右孩子入队。而后每次队列中一个结点出队，都将其左孩子和右孩子入队，直到树中所有结点都出队，出队结点的先后顺序就是层次遍历的最终结果。

img

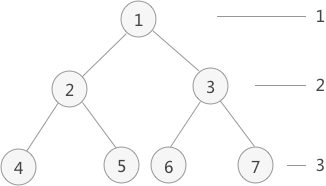
BFS和DFS

比较BFS和DFS

Breadth First Search（广度优先搜索），将相邻的节点一层层查找，找到最多的。

Deep FIrst Search（深度优先搜索），一直往下寻找，若没有剩余相邻节点时，回走一步，再查找剩余的下一个相邻节点，直到回到起始点

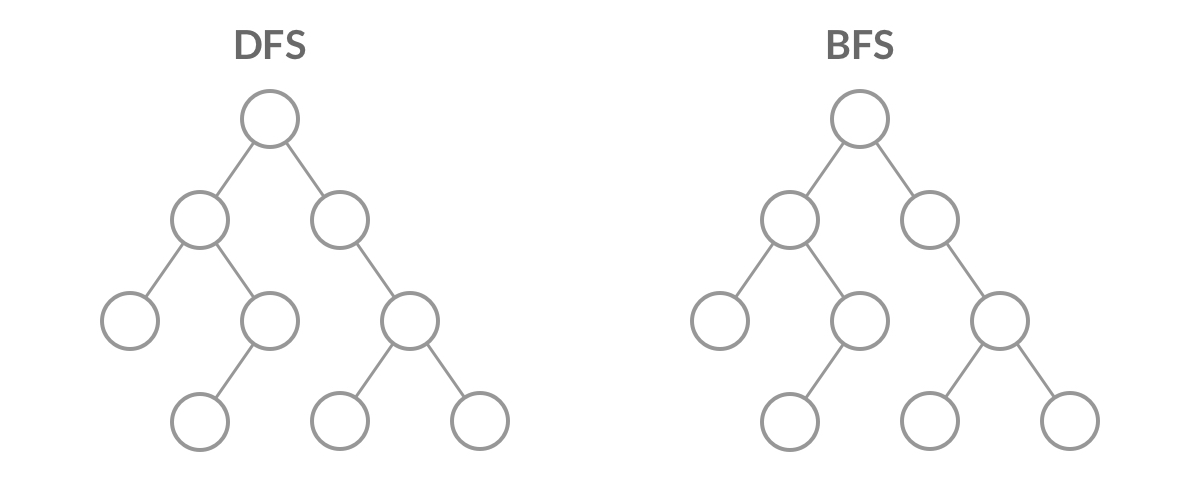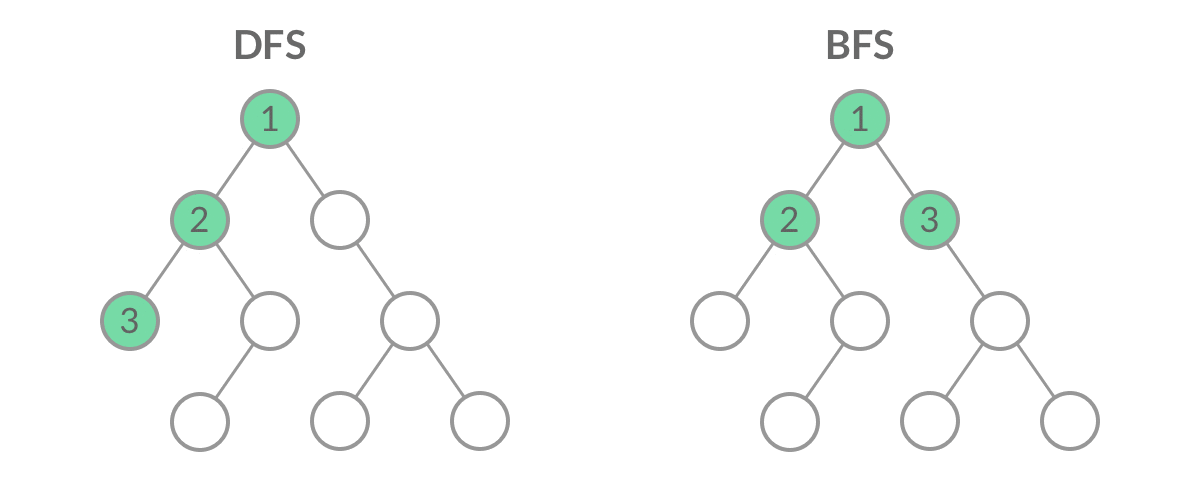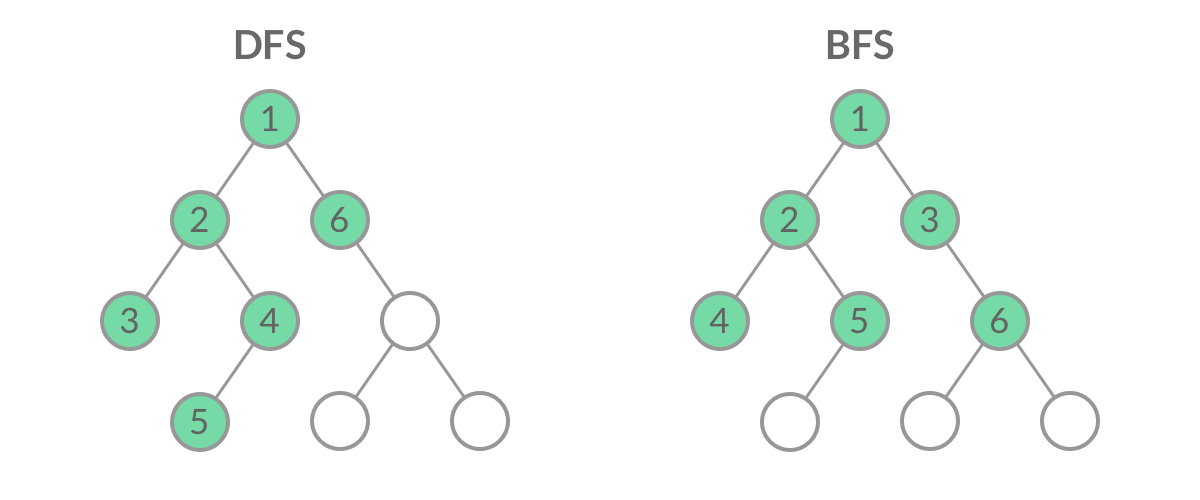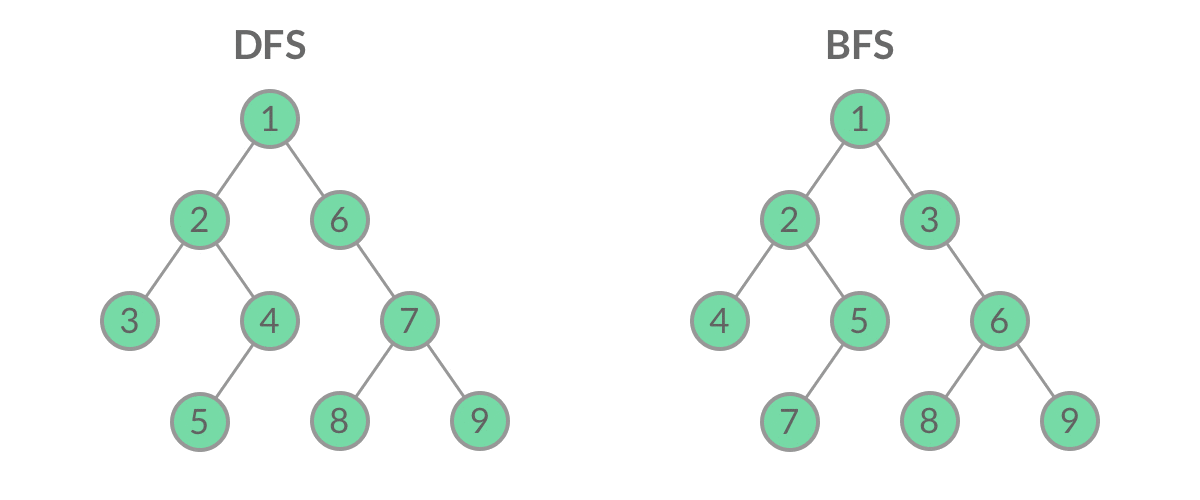
DFS（深度优先搜索）和 BFS（广度优先搜索）就像孪生兄弟，提到一个总是想起另一个。然而在实际使用中，我们用 DFS 的时候远远多于 BFS。那么，是不是 BFS 就没有什么用呢？

如果我们使用 DFS/BFS 只是为了遍历一棵树、一张图上的所有结点的话，那么 DFS 和 BFS 的能力没什么差别，我们当然更倾向于更方便写、空间复杂度更低的 DFS 遍历。不过，某些使用场景是 DFS 做不到的，只能使用 BFS 遍历。

DFS 与 BFS在二叉树上进行 DFS 遍历和 BFS 遍历的代码比较。

DFS 遍历使用递归：

1
2
3
4
5
6
7
8
9
void dfs(TreeNode root)
{
    if (root == null)
    {
        return;
    }
    dfs(root.left);
    dfs(root.right);
}

BFS 遍历使用队列数据结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
void bfs(TreeNode root) {
    Queue<TreeNode> queue = new Queue<TreeNode>();
    queue.Enqueue(root);// C# 的 add 写作 Enqueue()
    while (!queue.isEmpty()) {
        TreeNode node = queue.Dequeue(); // C# 的 pop 写作 Dequeue()
        if (node.left != null) {
            queue.Enqueue(node.left);
        }
        if (node.right != null) {
            queue.Enqueue(node.right);
        }
    }
}

只是比较两段代码的话，最直观的感受就是：DFS 遍历的代码比 BFS 简洁太多了！这是因为递归的方式隐含地使用了系统的 栈，我们不需要自己维护一个数据结构。如果只是简单地将二叉树遍历一遍，那么 DFS 显然是更方便的选择。

DFS 与 BFS 对比

BFS 的应用：层序遍历

BFS 的层序遍历应用：

LeetCode 102. Binary Tree Level Order Traversal 二叉树的层序遍历（Medium）

给定一个二叉树，返回其按层序遍历得到的节点值。 层序遍历即逐层地、从左到右访问所有结点。

什么是层序遍历呢？简单来说，层序遍历就是把二叉树分层，然后每一层从左到右遍历：

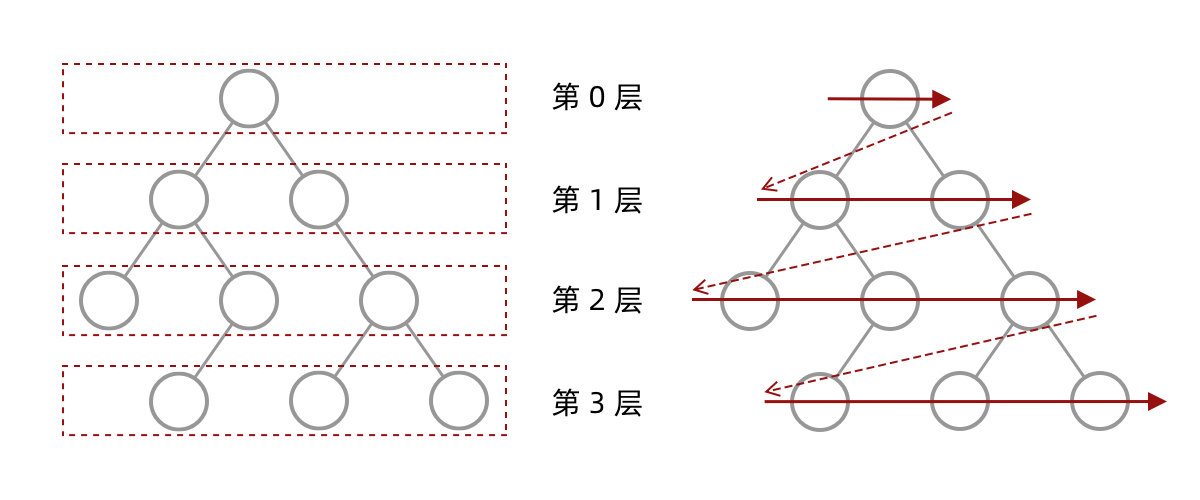
二叉树的层序遍历

乍一看来，这个遍历顺序和 BFS 是一样的，我们可以直接用 BFS 得出层序遍历结果。然而，层序遍历要求的输入结果和 BFS 是不同的。层序遍历要求我们区分每一层，也就是返回一个二维数组。而 BFS 的遍历结果是一个一维数组，需要稍微修改一下代码，在每一层遍历开始前，先记录队列中的结点数量 Count（也就是这一层的结点数量），然后一口气处理完这一层的 Count 个结点。

img

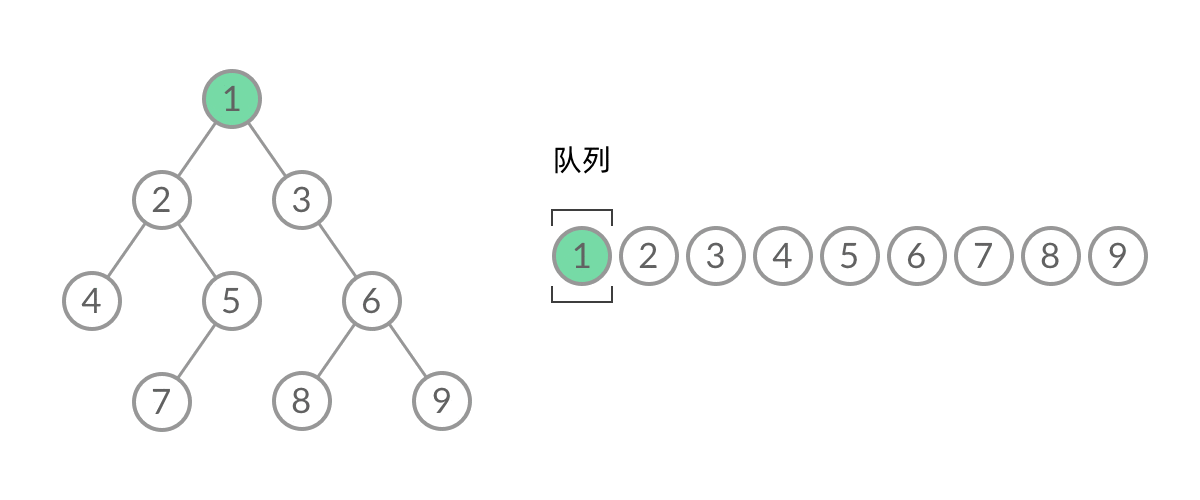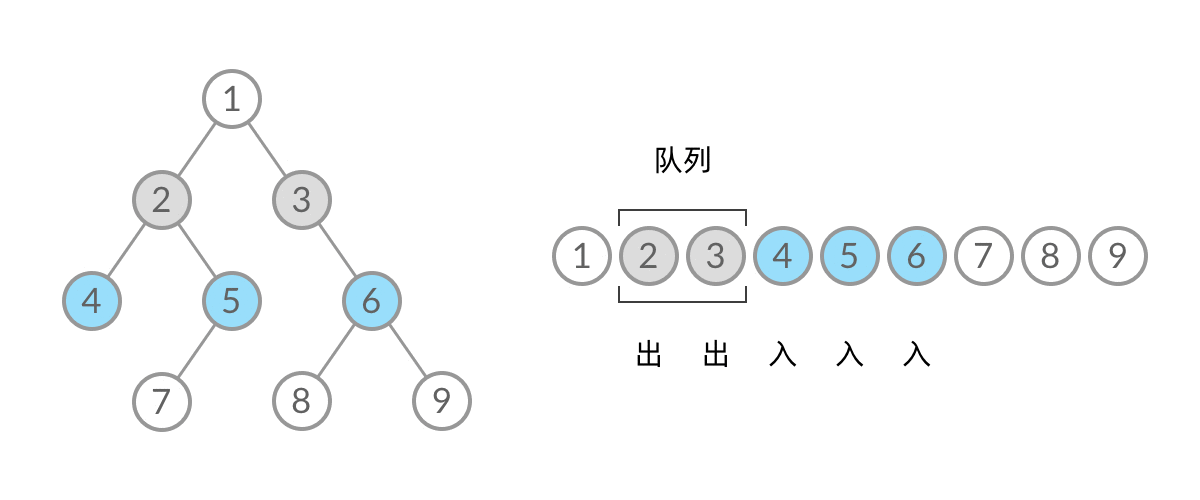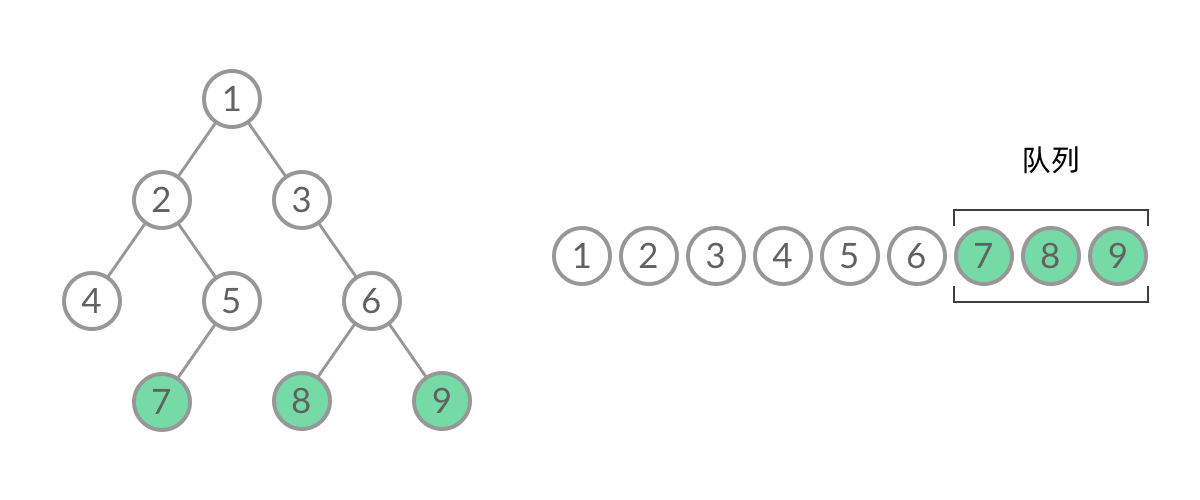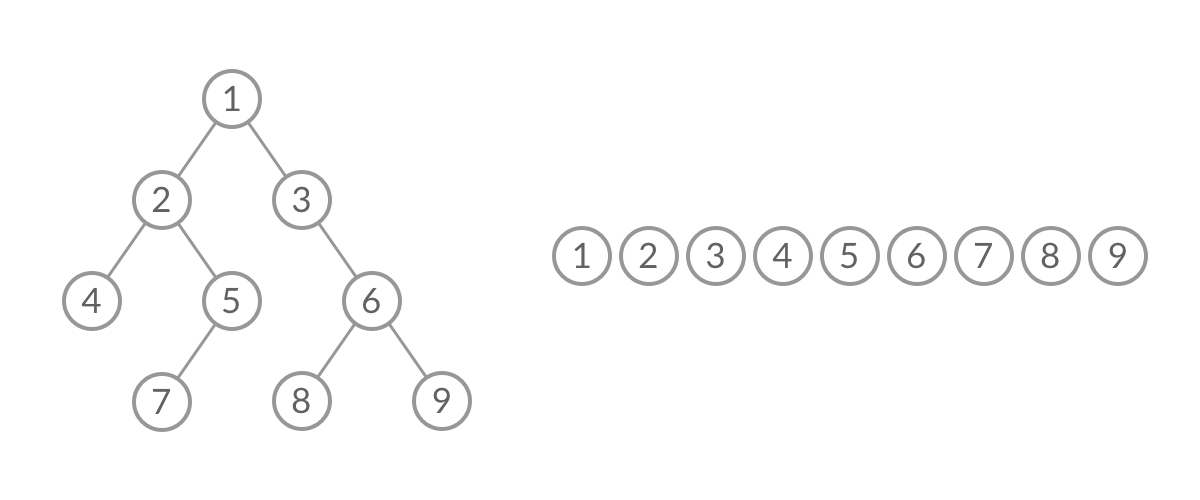
在 while 循环的每一轮中，都是将当前层的所有结点出队列，再将下一层的所有结点入队列，这样就实现了层序遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public IList<IList<int>> LevelOrder(TreeNode root) {
    IList<IList<int>> result = new List<IList<int>>();
    if(root == null) return result;
    IList<int> ans = new List<int>();
    Queue<TreeNode> queue = new Queue<TreeNode>();
    int len = 0;
    queue.Enqueue(root);
    while (queue.Count != 0)
    {
        len = queue.Count;
        ans.Clear();
      	for (int i = 0; i < len; i++)
        {
          	TreeNode node = queue.Dequeue();
          	ans.Add(node.val);
          	if(node.left!=null) queue.Enqueue(node.left);
          	if(node.right!=null) queue.Enqueue(node.right);
        }
      	result.Add(new List<int>(ans));
   	 }
 		 return result;
}

DFS的应用：回溯算法